Cyril Marzouk
École polytechnique
Centre de Mathématiques Appliquées - UMR 7641 CNRS
Route de Saclay
91128 Palaiseau Cedex
Email : cyril (dot) marzouk (at) polytechnique (dot) edu
Office : 00 30 23 (wing 0, 2nd floor)
Phone : +33 (0) 1 69 33 45 78
Cyril MarzoukÉcole polytechnique Centre de Mathématiques Appliquées - UMR 7641 CNRS Route de Saclay 91128 Palaiseau Cedex Email : cyril (dot) marzouk (at) polytechnique (dot) edu Office : 00 30 23 (wing 0, 2nd floor) Phone : +33 (0) 1 69 33 45 78 |
|
|
|
|
|
|
|
I am a probabilist mainly interested in the behaviour of large random discrete combinatorial objects such as trees, laminations, and maps. Below is the list in reverse chronological order of my papers, they are all available by simply clicking on the title; see also arXiv, Hal, or zbMATH.
The articles 5 to 15 are also decribed in my habilitation thesis entitled A few aspects of large random maps, defended the 1st of December 2022 at École polytechnique.
| Abstract: Motivated by scaling limits of random planar maps in random geometry, we introduce and study Lévy looptrees and Lévy maps. They are defined using excursions of general Lévy processes with no negative jump and extend the known stable looptrees and stable maps, associated with stable processes. We compute in particular their fractal dimensions in terms of the upper and lower Blumenthal–Getoor exponents of the coding Lévy process. In a second part, we consider excursions of stable processes with a drift and prove that the corresponding looptrees interpolate continuously as the drift varies from $-\infty$ to $\infty$, or as the self-similarity index varies from $1$ to $2$, between the Brownian tree and a circle, whereas the corresponding maps interpolate between the Brownian sphere and the Brownian tree. |
|
| Abstract: We first rephrase and unify known bijections between bipartite plane maps and labelled trees with the formalism of looptrees, which we argue to be both more relevant and technically simpler since the geometry of a looptree is explicitly encoded by the depth-first walk (or Łukasiewicz path) of the tree, as opposed to the height or contour process for the tree. We then construct continuum analogues associated with any càdlàg path with no negative jump and derive several invariance principles. We especially focus on uniformly random looptrees and maps with prescribed face degrees and study their scaling limits in the presence of macroscopic faces, which complements a previous work in the case of no large faces. The limits (along subsequences for maps) form new families of random metric measured spaces related to processes with exchangeable increments with no negative jumps and our results generalise previous works which concerned the Brownian and stable Lévy bridges. |
|
| Abstract: We investigate the structure of large uniform random maps with a given number of vertices, edges, faces and on a surface of a given genus. We focus on two regimes: the planar case and the unicellular case, letting the three other parameters tend to infinity in a sparse regime, in which the ratio between the number of vertices and edges tends to $1$. Albeit different at first sight, these two models can be treated in a unified way, using a probabilistic version of the classical core--kernel decomposition. In both cases, we identify a mesoscopic scale at which the scaling limits of these random maps can be obtained by first taking the local limit of their kernels (or scheme) -- which turns out to be the dual of the Uniform Infinite Planar Triangulation in the planar case and the infinite three-regular tree in the unicellular case -- and then replacing each edge by an independent (mass-biased) Brownian tree with two marked points. |
|
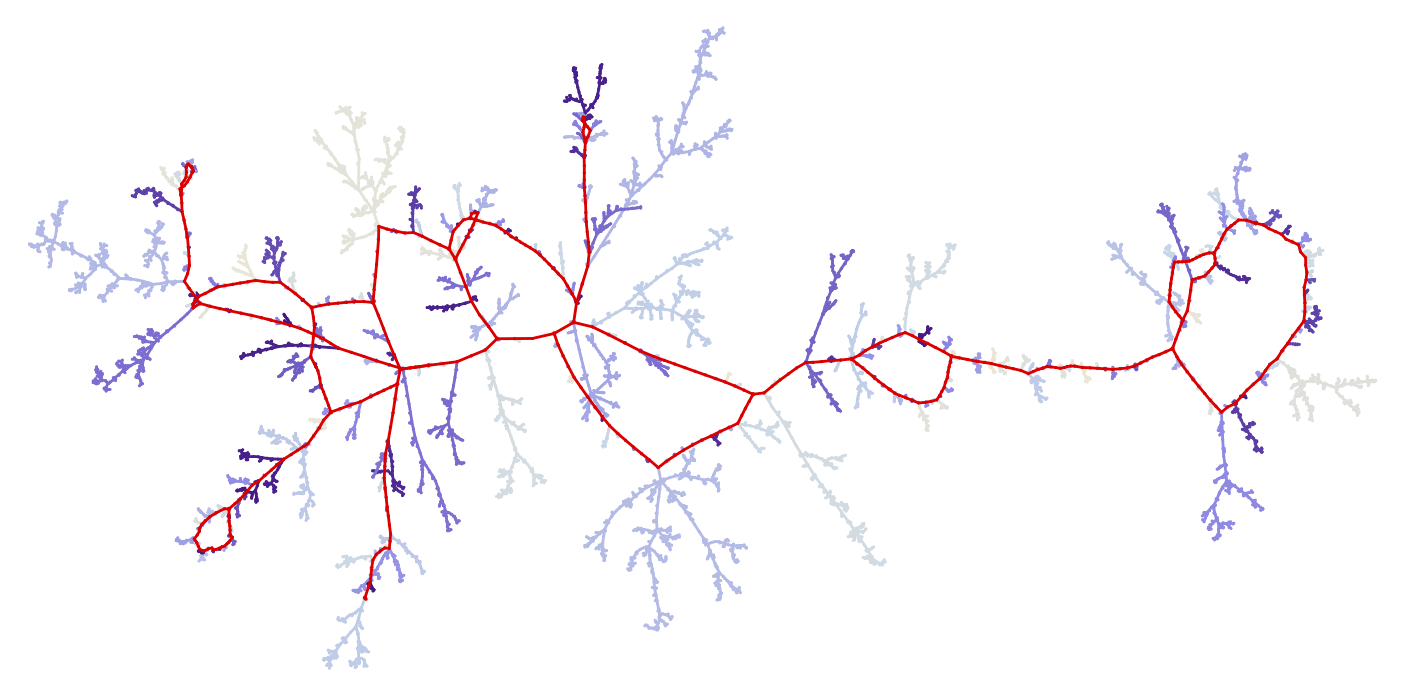
| Abstract: We first establish new local limit estimates for the probability that a nondecreasing integer-valued random walk lies at time $n$ at an arbitrary value, encompassing in particular large deviation regimes. This enables us to derive scaling limits of such random walks conditioned by their terminal value at time $n$ in various regimes. We believe both to be of independent interest. We then apply these results to obtain invariance principles for the Łukasiewicz path of Bienaymé–Galton–Watson trees conditioned on having a fixed number of leaves and of vertices at the same time, which constitutes a first step towards understanding their large scale geometry. We finally deduce from this scaling limit theorems for random bipartite planar maps under a new conditioning by fixing their number of vertices, edges, and faces at the same time. In the particular case of the uniform distribution, our results confirm a prediction of Fusy & Guitter on the growth of the typical distances and show furthermore that in all regimes, the scaling limit is the celebrated Brownian map. |
|
| Abstract: The infinite discrete stable Boltzmann maps are generalisations of the well-known Uniform Infinite Planar Quadrangulation in the case where large degree faces are allowed. We show that the simple random walk on these random lattices is always subdiffusive with exponent less than $1/3$. Our method is based on stationarity and geometric estimates obtained via the peeling process which are of own interest. |
|
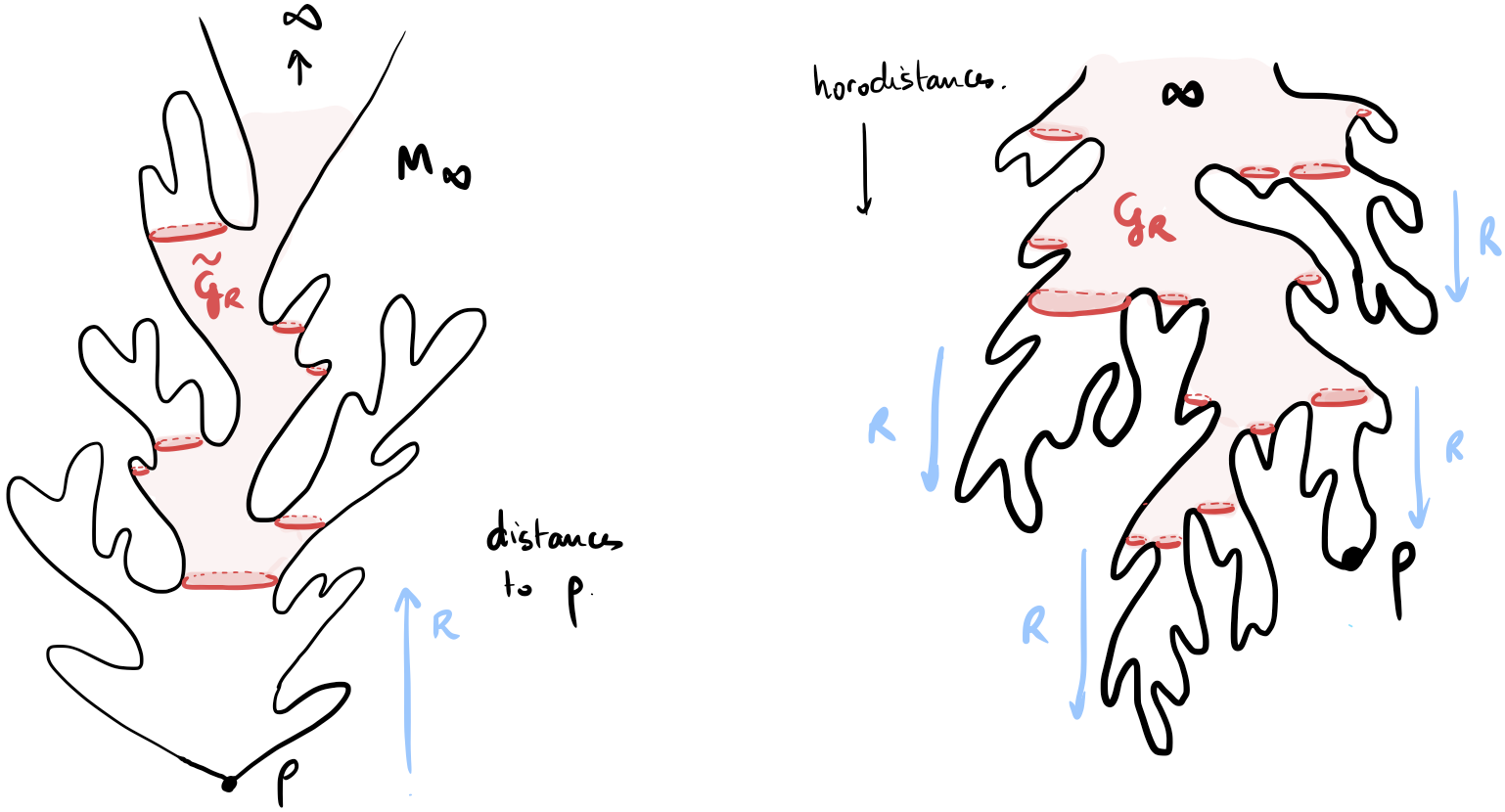
| Abstract: We study a configuration model on bipartite planar maps in which, given $n$ even integers, one samples a planar map with $n$ faces uniformly at random with these face degrees. We prove that when suitably rescaled, such maps always admit nontrivial subsequential limits as $n \to \infty$ in the Gromov--Hausdorff--Prokhorov topology. Further, we show that they converge in distribution towards the celebrated Brownian sphere, and more generally a Brownian disk for maps with a boundary, if and only if there is no inner face with a macroscopic degree, or, if the perimeter is too big, the maps degenerate and converge to the Brownian tree. By first sampling the degrees at random with an appropriate distribution, this model recovers that of size-conditioned Boltzmann maps associated with critical weights in the domain of attraction of a stable law with index $\alpha\in [1,2]$. The Brownian tree and disks then appear respectively in the case $\alpha=1$ and $\alpha=2$, whereas in the case $\alpha \in (1,2)$ our results partially recover previous known ones. Our proofs rely on known bijections with labelled plane trees, which are similarly sampled uniformly at random given $n$ outdegrees. Along the way, we obtain some results on the geometry of such trees, such as a convergence to the Brownian tree but only in the weaker sense of subtrees spanned by random vertices, which are of independent interest. |
|
| Abstract: The infinite discrete stable Boltzmann maps are "heavy-tailed" generalisations of the well-known Uniform Infinite Planar Quadrangulation. Very efficient tools to study these objects are Markovian step-by-step explorations of the lattice called peeling processes. Such a process depends on an algorithm which selects at each step the next edge where the exploration continues. We prove here that, whatever this algorithm, a peeling process always reveals about the same portion of the map, thus growing roughly metric balls. Applied to well-designed algorithms, this easily enables us to compare distances in the map and in its dual, as well as to control the so-called pioneer points of the simple random walk, both on the map and on its dual. |
|
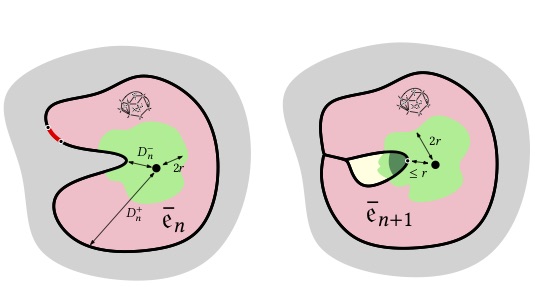
| Abstract: We discuss the asymptotic behaviour of random critical Boltzmann planar maps in which the degree of a typical face belongs to the domain of attraction of a stable law with index $\alpha \in (1,2]$. We prove that when conditioning such maps to have $n$ vertices, or $n$ edges, or $n$ faces, the vertex-set endowed with the graph distance suitably rescaled converges in distribution towards the celebrated Brownian map when $\alpha=2$, and, after extraction of a subsequence, towards another '$\alpha$-stable map' when $\alpha < 2$, which improves on a first result due to Le Gall & Miermont who assumed slightly more regularity. |
|
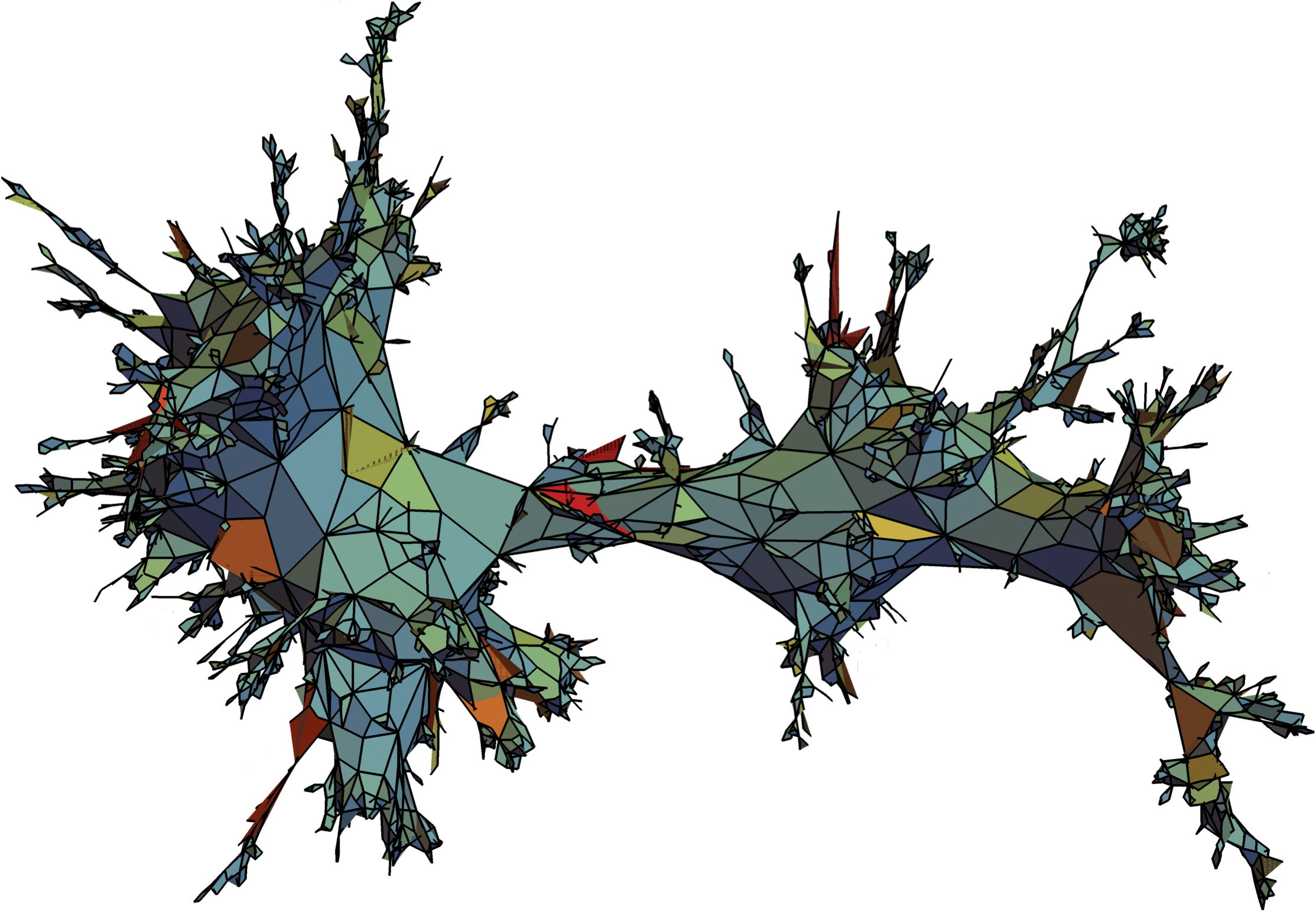
| Abstract: We consider so-called discrete snakes obtained from size-conditioned critical Bienaymé–Galton–Watson trees by assigning to each node a random spatial position in such a way that the increments along each edge are i.i.d. When the offspring distribution belongs to the domain of attraction of a stable law with index $\alpha \in (1,2]$, we give a necessary and sufficient condition on the tail distribution of the spatial increments for this spatial tree to converge, in a functional sense, towards the Brownian snake driven by the $\alpha$-stable Lévy tree. We also study the case of heavier tails, and apply our result to study the number of inversions of a uniformly random permutation indexed by the tree. |
|
| Abstract: The peeling process is an algorithmic procedure that discovers a random planar map step by step. In generic cases such as the UIPT or the UIPQ, it is known [Curien & Le Gall, Scaling limits for the peeling process on random maps, Ann. Inst. Henri Poincaré Probab. Stat. 53, 1 (2017), 322–357] that any peeling process will eventually discover the whole map. In this paper we study the probability that the origin is not swallowed by the peeling process until time $n$ and show it decays at least as $n^{-2c/3}$ where \[c \approx 0.12831235141783245423674486573872854933142662048339843...\] is defined via an integral equation derived using the Lamperti representation of the spectrally negative $3/2$-stable Lévy process conditioned to remain positive [Chaumont, Kyprianou & Pardo, Some explicit identities associated with positive self-similar Markov processes, Stochastic Process. Appl. 119, 3 (2009), 980–1000] which appears as a scaling limit for the perimeter process. As an application we sharpen the upper bound of the sub-diffusivity exponent for random walk of [Benjamini & Curien, Simple random walk on the uniform infinite planar quadrangulation: subdiffusivity via pioneer points, Geom. Funct. Anal. 23, 2 (2013), 501–531]. |
|
| Abstract: We study the geometry of infinite random Boltzmann planar maps having weight of polynomial decay of order $k^{-2}$ for each vertex of degree $k$. These correspond to the dual of the discrete "stable maps" of Le Gall and Miermont [Scaling limits of random planar maps with large faces, Ann. Probab. 39, 1 (2011), 1-69] studied in [Budd & Curien, Geometry of infinite planar maps with high degrees, Electron. J. Probab. 22 (2017), Paper No. 35, 37p.] related to a symmetric Cauchy process, or alternatively to the maps obtained after taking the gasket of a critical $O(2)$-loop model on a random planar map. We show that these maps have a striking and uncommon geometry. In particular we prove that the volume of the ball of radius $r$ for the graph distance has an intermediate rate of growth and scales as $\mathrm{e}^{\sqrt{r}}$. We also perform first passage percolation with exponential edge-weights and show that the volume growth for the fpp-distance scales as $\mathrm{e}^{r}$. Finally we consider site percolation on these lattices: although percolation occurs only at $p=1$, we identify a phase transition at $p=1/2$ for the length of interfaces. On the way we also prove new estimates on random walks attracted to an asymmetric Cauchy process. |
|
| Abstract: We study the asymptotic behaviour of uniform random maps with a prescribed face-degree sequence, in the bipartite case, as the number of faces tends to infinity. Under mild assumptions, we show that, properly rescaled, such maps converge in distribution towards the Brownian map in the Gromov-Hausdorff sense. This result encompasses a previous one of Le Gall for uniform random q-angulations where q is an even integer. It applies also to random maps sampled from a Boltzmann distribution, under a second moment assumption only, conditioned to be large in either of the sense of the number of edges, vertices, or faces. The proof relies on the convergence of so-called "discrete snakes" obtained by adding spatial positions to the nodes of uniform random plane trees with a prescribed child sequence recently studied by Broutin & Marckert. This paper can alternatively be seen as a contribution to the study of the geometry of such trees. |
|
| Abstract: We study the asymptotic behaviour of random simply generated noncrossing planar trees in the space of compact subsets of the unit disk, equipped with the Hausdorff distance. Their distributional limits are obtained by triangulating at random the faces of stable laminations, which are random compact subsets of the unit disk made of non-intersecting chords and which are coded by stable Lévy processes. We also study other ways to "fill-in" the faces of stable laminations, which leads us to introduce the iteration of laminations and of trees. |
|
| Abstract: We introduce and study the model of simply generated non-crossing partitions, which are, roughly speaking, chosen at random according to a sequence of weights. This framework encompasses the particular case of uniform non-crossing partitions with constraints on their block sizes. Our main tool is a bijection between non-crossing partitions and plane trees, which maps such simply generated non-crossing partitions into simply generated trees so that blocks of size $k$ are in correspondence with vertices of out-degree $k$. This allows us to obtain limit theorems concerning the block structure of simply generated non-crossing partitions. We apply our results in free probability by giving a simple formula relating the maximum of the support of a compactly supported probability measure on the real line in term of its free cumulants. |
|
